Let's use TRACE to identify where these values of x are. Since the y-values of the two functions are equal at the intersection point, the x-values we want must be either to the left or to the right of this point. While in TRACE, use the up arrow or down arrow keys to move back and forth between the graphs. Do this at several places on each side of the intersection point and compare the Y1 and Y2 y-values. The x-values to the right of -1.75 produce y-values for Y1 that
are greater than those of Y2. The inequality |
|
| Copyright © 2010 Turner Educational Publishing
|
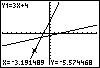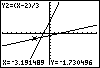

 means that the graph of Y1 must lie above the graph of
Y2. Looking at the graphs, we see this is true if x is to the right of the
intersection point, meaning to the right of -1.75. So, the solution set is
means that the graph of Y1 must lie above the graph of
Y2. Looking at the graphs, we see this is true if x is to the right of the
intersection point, meaning to the right of -1.75. So, the solution set is 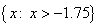 , or in interval notation,
, or in interval notation, 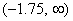 .
.