We now interpret the inequality  in terms of the function that is graphed. The solution set will be all values of x for which the
function Y1 has negative y-values. Let's use TRACE to identify where these values of
x are.
in terms of the function that is graphed. The solution set will be all values of x for which the
function Y1 has negative y-values. Let's use TRACE to identify where these values of
x are.Since the x-intercept has a y-value equal to 0, it is NOT part of the solution set. The
x-values to the left of 3 produce negative y-values. The inequality |
|
| Copyright © 2010 Turner Educational Publishing
|
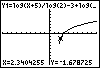

 , or in interval notation, (2, 3).
, or in interval notation, (2, 3).