We now interpret the inequality Since the x-intercepts have a y-value equal to 0, they are NOT
part of the solution set. The x-values to the left of -2 yield negative y-values.
The values of x between -2 and 2/3, and to the right of 2/3, produce
positive y-values. The inequality |
|
| Copyright © 2010 Turner Educational Publishing
|
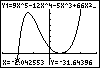

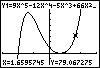
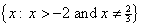 , or in interval notation,
, or in interval notation,