|
We now interpret the inequality 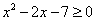 in terms of the function we have graphed. The solution set will be
all values of x for which the function Y1 has positive or zero y-values.
Let's use TRACE to identify where these values of x are. in terms of the function we have graphed. The solution set will be
all values of x for which the function Y1 has positive or zero y-values.
Let's use TRACE to identify where these values of x are.
Since the x-intercepts have a y-value of 0, they are part of the
solution set. The x-values to the left of -1.83 yield positive y-values,
as well as the x-values to the right of 3.83. The inequality 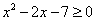 means that the graph
of Y1 (the parabola) must lie on or above the x-axis. Looking at the
graph, we observe this is true if x is to the left of -1.83 or to the right
of 3.83. So, the solution set is approximately means that the graph
of Y1 (the parabola) must lie on or above the x-axis. Looking at the
graph, we observe this is true if x is to the left of -1.83 or to the right
of 3.83. So, the solution set is approximately 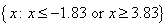 , or in interval notation, , or in interval notation, ![(-infinity, -1.83]U[3.83, infinity)](page7e.gif) . . |

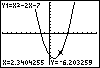

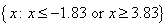 , or in interval notation,
, or in interval notation,