Since the x-intercept has a y-value equal to 0, it is part of the solution set. The x-values (on the first branch) to the left of the vertical asymptote x = -1 yield negative y-values. The values of x (on the right branch) between the vertical asymptote and the intercept x = 4 produce positive y-values. The x-values to the right of the intercept again yield negative y-values. The inequality |
|
| Copyright © 2010 Turner Educational Publishing
|
means that the
graph of Y1 must lie on or above the x-axis. By observing the graph, we see this is true
if x is between -1 and 4, including x = 4 but not including x = -1 (because the function is
undefined). So, the solution set is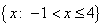 
, or in interval notation, (-1, 4].
