Next we will graph the first twelve terms of the recursively defined sequence 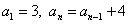 . This is an example of an arithmetic
sequence. First define the sequence as u in the sequence editor. Be sure nMin = 1, then define
the rule for the sequence on the next line. Enter . This is an example of an arithmetic
sequence. First define the sequence as u in the sequence editor. Be sure nMin = 1, then define
the rule for the sequence on the next line. Enter 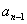 as u(n-1), which refers to the previous term in the
sequence. For a recursively defined sequence you must also specify u(nMin), which represents the
first term as u(n-1), which refers to the previous term in the
sequence. For a recursively defined sequence you must also specify u(nMin), which represents the
first term 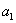 . For this
example the first term is 3, so set u(nMin)=3. . For this
example the first term is 3, so set u(nMin)=3.
From the sequence definition we can conclude that the smallest term will be the first term, and all following terms will increase by four. It would be helpful to know the twelfth term so we can set Ymax properly. |
|||
| Copyright © 2010 Turner Educational Publishing
|
