We now interpret the inequality 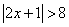 in terms of the two functions we have graphed. The solution set will be all values of x for
which the absolute value function Y1 has y-values greater than those of the constant function
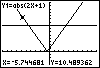
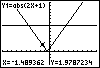
Y2. Let's use TRACE to identify where these values of x are. Since the y-values of the two
functions are equal at the intersection points, the x-values we want must be either to the left
or to the right of these points. Use the up or down arrow keys to move back and forth between
the graphs and compare the y-values at several places.
in terms of the two functions we have graphed. The solution set will be all values of x for
which the absolute value function Y1 has y-values greater than those of the constant function
Y2. Let's use TRACE to identify where these values of x are. Since the y-values of the two
functions are equal at the intersection points, the x-values we want must be either to the left
or to the right of these points. Use the up or down arrow keys to move back and forth between
the graphs and compare the y-values at several places.The inequality |
|
| Copyright © 2010 Turner Educational Publishing
|

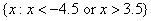 , or in interval notation,
, or in interval notation,