INEQUALITIES (2 VARIABLES) Linear Programming (Page 1 of 7)

An application involving systems of linear inequalities is linear programming. As an example, let's find the minimum and maximum values of the objective function C = 4x + 3y subject to the constraints 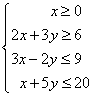x >= 0, 2x+3y >= 6, 3x-2y <= 9, x+5y <= 20.

First we must identify the feasible solution set, which is the solution set to the system of inequalities representing the constraints. The solution set to the first inequality is the right half-plane. For the other three inequalities, isolate y:
                                              y >= -(2/3)x+2, y >= 1.5x-4.5, y <= -0.2x+4.

The corresponding boundary equations are
                                              y = -(2/3)x+2, y = 1.5x-4.5, y = -0.2x+4.
Copyright © 2010 Turner Educational Publishing
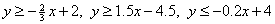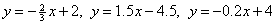Go back to the previous page. Go to the next page. Go to the Table of Contents. Go to the Index page. Go to the Quiz page. Exit to the Home page.