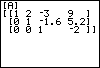SYSTEMS OF EQUATIONS Gauss-Jordan Reduction (Page 1 of 7)

With Gauss-Jordan reduction, we continue the elimination process on the augmented matrix, going beyond row-echelon form until we have obtained reduced row-echelon form. The steps are very similar to those we have already performed.

Let's continue the previous example with Gauss-Jordan reduction. The augmented matrix is in row-echelon form, and is stored as matrix A. Begin by reviewing the contents of this matrix.

CLEAR key.

MATRX key. 1: menu selection. ENTER key. **

 Calculator screen image.

Column one is in reduced row-echelon form, but columns two and three are not. We must eliminate the 2 in the first position of column two.
Copyright © 2010 Turner Educational Publishing
Go back to the previous page. Go to the next page. Go to the Table of Contents. Go to the Index page. Go to the Quiz page. Exit to the Home page.