COMPLEX NUMBERS Polar Form Conversions (Page 4 of 11)

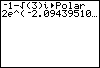
A second method of converting a complex number from rectangular to polar form is the Polar command located in the MATH CPX submenu. The advantage of this method is that we can get the modulus and the argument with a single command. The result will be displayed using Euler notation (the TI-83/84 does not use rcisθ notation).

Let's use the same complex number again, -1-sqrt(3)*i, and try this new method. We will leave the calculator in radian mode. This time, we enter the complex number first, and then follow it with the command.

 CLEAR key.

 Negation key. 1 Minus key. 2nd Square root key. 3 Right parenthesis key. 2nd i key. MATH key. [CPX] 7: menu selection. ENTER key.

 Calculator screen image.

The coefficient of the base e is the modulus (2 in this case), and the coefficient of i in the exponent position is the argument (in radians). Press the right arrow key to scroll to the right in order to see the rest of the answer. Observe that these results agree with our earlier work in this topic.
Copyright © 2010 Turner Educational Publishing
Go back to the previous page. Go to the next page. Go to the Table of Contents. Go to the Index page. Go to the Quiz page. Exit to the Home page.