IDENTITIES Verifying Identities (Page 4 of 5)

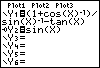
Recall that an identity is an equation that holds true for all values of x for which the equation is defined. Since this equation involves the secant and cosecant function, it is not defined for multiples of π/2 (the cosecant function is not defined for even multiples of π/2 and the secant function is not defined for odd multiples of π/2). Because the table seems to confirm that the two expressions agree for all other values of x, the equation appears to be an identity.

To verify the identity graphically, we will graph the two expressions together and compare their graphs. First, change the style of function Y2 to "Path" which will draw the graph of Y2 while tracing it with a visual marker. This will allow us to observe the second graph being drawn even if it overlaps the graph of Y1.

 Y= key.

 Left arrow key. Left arrow key. Down arrow key.
 ENTER key. (four times)

 Calculator screen image.
Copyright © 2010 Turner Educational Publishing
Go back to the previous page. Go to the next page. Go to the Table of Contents. Go to the Index page. Go to the Quiz page. Exit to the Home page.